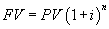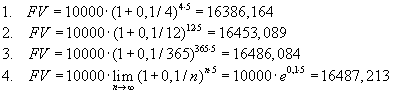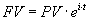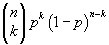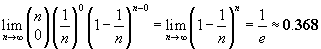V minulém příspěvku jsem poukázal na krásné vyjádření Eulerova čísla pomocí limity či nekonečného součtu. Eulerovo číslo se vyskytuje poměrně často v mnoha oborech. V tomto článku poukáži na podle mého názoru dva nejzajímavější příklady.
Troufám si tvrdit, že řada lidí by nehledala Eulerovo číslo ve finančnictví, ale ono tam je - ve složeném úročení.
Řekněme, že si někdo dá 10 000 Kč na nějaký termínovaný vklad s roční úrokovou mírou 10% a ročním připisováním úroků na dobu 5 let. Pak na konci pětiletého období bude mít na účtu (pomineme-li pro zjednodušení zdanění úroků) 10 000× 1,15 =16105,1 Kč. Matematicky lze složené úročení popsat jednoduchou rovnicí
kde
FV je budoucí hodnota investovaných peněz,
PV současná hodnota a
i úroková míra. Vraťme se k našemu příkladu a uvažujme situace, kdy dochází k připisování úroků
- čtvrtletně,
- měsíčně,
- denně,
- nepřetržitě.
Použitím posledně uvedeného vzorce získáme následující výsledky
Poslední případ, kdy dochází k nepřetržitému přidávání úroku k jistině, se nazývá spojité úročení:
kde
e je Eulerovo číslo,
t počet let a
i úroková míra spjatá s každým přípisem úroku (tedy
i je např. čtvrtina roční nominální úrokové míry). Všimněme si, že denní úročení se dosti podobá svým výsledkem spojitému úročení. Z příkladu plyne, že bychom si u různých finančních produktů, jako jsou např. spořící účty měli všímat četnosti připisování úroků, neboť s vyšší četností dosáhneme většího výdělku.
Číslo
e se vyskytuje i v teorii pravděpodobnosti.
Příklad: Uvažujme hráče u herního automatu, u kterého nastává výhra jednou za
n her. A nechť tento hráč bude hrát právě
n her. Potom pro velká
n platí, že pravděpodobnost, že hráč nevyhraje ani jednu hru ze všech
n her je rovna 1/
e.
Tato úloha z teorie pravděpodobnosti je klasickým příkladem tzv.
Bernoulliho procesu, kdy se mnohokrát (
n-krát) opakuje situace, u které může nastat pouze jedna ze dvou možností, z nichž jednu chápeme jako výhru a druhou jako prohru. Uvažme například situaci, kdy
n-krát házíme jednou mincí. Jako výhru v každém hodu chápejme situaci, kdy padne líc. A nechť pravděpodobnost výhry (padl líc) je rovna
p. Potom pravděpodobnost, že vyhrajeme
k-krát ze všech
n-pokusů je rovna
Vraťme se k našemu příkladu; ze zadání plyne
n → ∞, k → 0. Nyní můžeme využít předcházejícího vzorce. Pravděpodobnost výhry v jednom hodu je
p=1/
n. Proto pravděpodobnost, že hráč nevyhraje ani jednu hru ze všech
n her je rovna
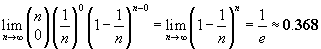
Eulerovo číslo se vyskytuje i mnoha dalších mnohem složitějších matematických problémech, ale tyto dva pěkné příklady názorně ukazují, že matematické konstanty se mohou vyskytovat i v mnoha problémech běžného života.