Mezi nejdůležitější matematické konstanty patří e, která se někdy nazývá Eulerova či Napierova konstanta. Matematika sice neobsahuje tolik význačných konstant jako fyzika, ale její konstanty jsou často pilířem určité ucelené teorie - např. imaginární jednotka i pro terorii komplexních čísel, 0 a 1 pro aritmetiku, či Ludolfovo číslo π pro geometrii.
Konstanta e, jejíž přibližná hodnota je 2,718281828459045235360287471352, se často definuje jako takové jediné reálné číslo a s vlastností, že funkce ax má hodnotu směrnice tečny v bodě 0 rovnu 1. První odkazy na tuto konstantu se objevují v roce 1618 v práci o logaritmických funkcích Johna Napiera. V této práci byla příloha, která obsahovala tabulku různých konstant a funkčních hodnot přirozených logaritmů. Ale samotný "objev" této konstanty se přisuzuje Jacobu Bernoullimu, který se zabýval výpočtem limity
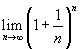
Podívejme se nyní na důkaz, že výše uvedená limita existuje a je rovna e. V důkazu využijeme známé nerovnosti mezi geometrickým a aritmetickým průměrem:
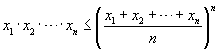
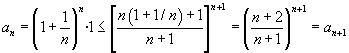
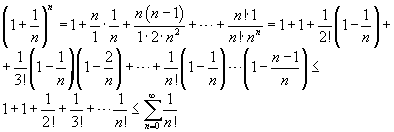
Zvolme m,n ∈ N, m ≤ n a rozepišme podobně jako výše výraz
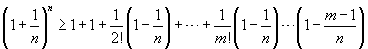
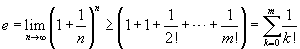
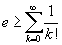
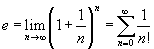
Eulerova konstanta má spoustu zajímavých vlastností a aplikací, o tom ale příště.
Poznámky



